Exploring Structured Semantic Priors Underlying Diffusion Score for Test-time Adaptation

  

Mingjia Li¹

  

Shuang Li^✉2

  

Tongrui Su¹

  

Longhui Yuan¹

  

Jian Liang³

  

Wei Li^✉4

¹ Beijing Institute of Technology

² Beihang University

³ Kuaishou Technology

⁴ Inceptio Technology

   ^✉ corresponding author

                        Abstract Capitalizing on the complementary advantages of generative and discriminative models has always been a compelling vision in machine learning, backed by a growing body of research. This work discloses the hidden semantic structure within score-based generative models, unveiling their potential as effective discriminative priors. Inspired by our theoretical findings, we propose DUSA to exploit the structured semantic priors underlying diffusion score to facilitate the test-time adaptation of image classifiers or dense predictors. Notably, DUSA extracts knowledge from a single timestep of denoising diffusion, lifting the curse of Monte Carlo-based likelihood estimation over timesteps. We demonstrate the efficacy of our DUSA in adapting a wide variety of competitive pre-trained discriminative models on diverse test-time scenarios. Additionally, a thorough ablation study is conducted to dissect the pivotal elements in DUSA. Method Overview

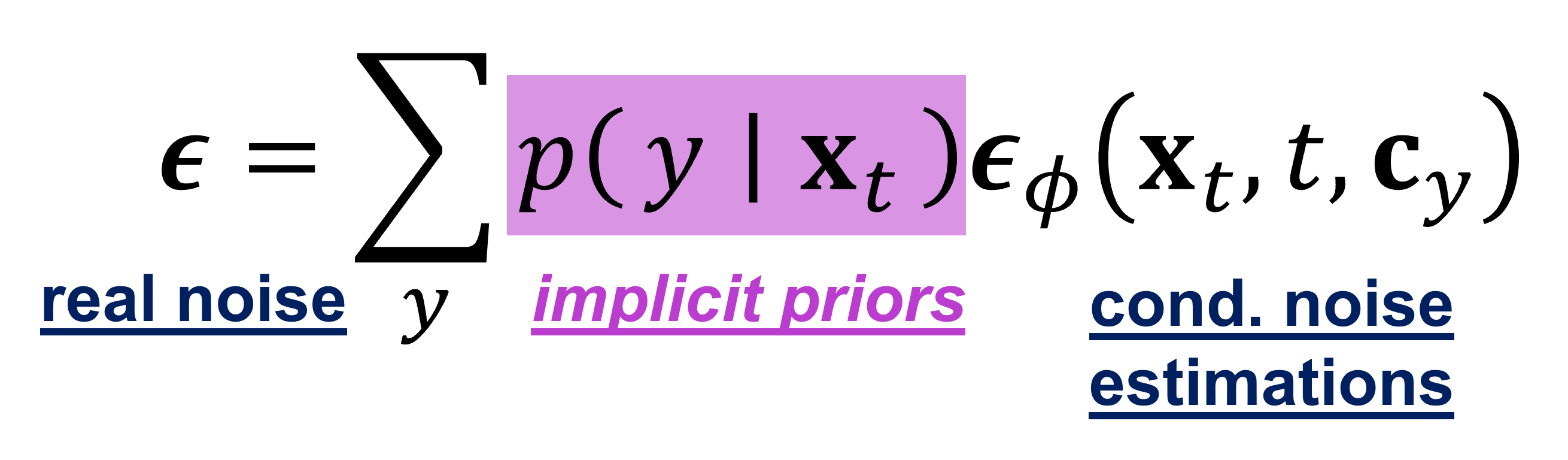
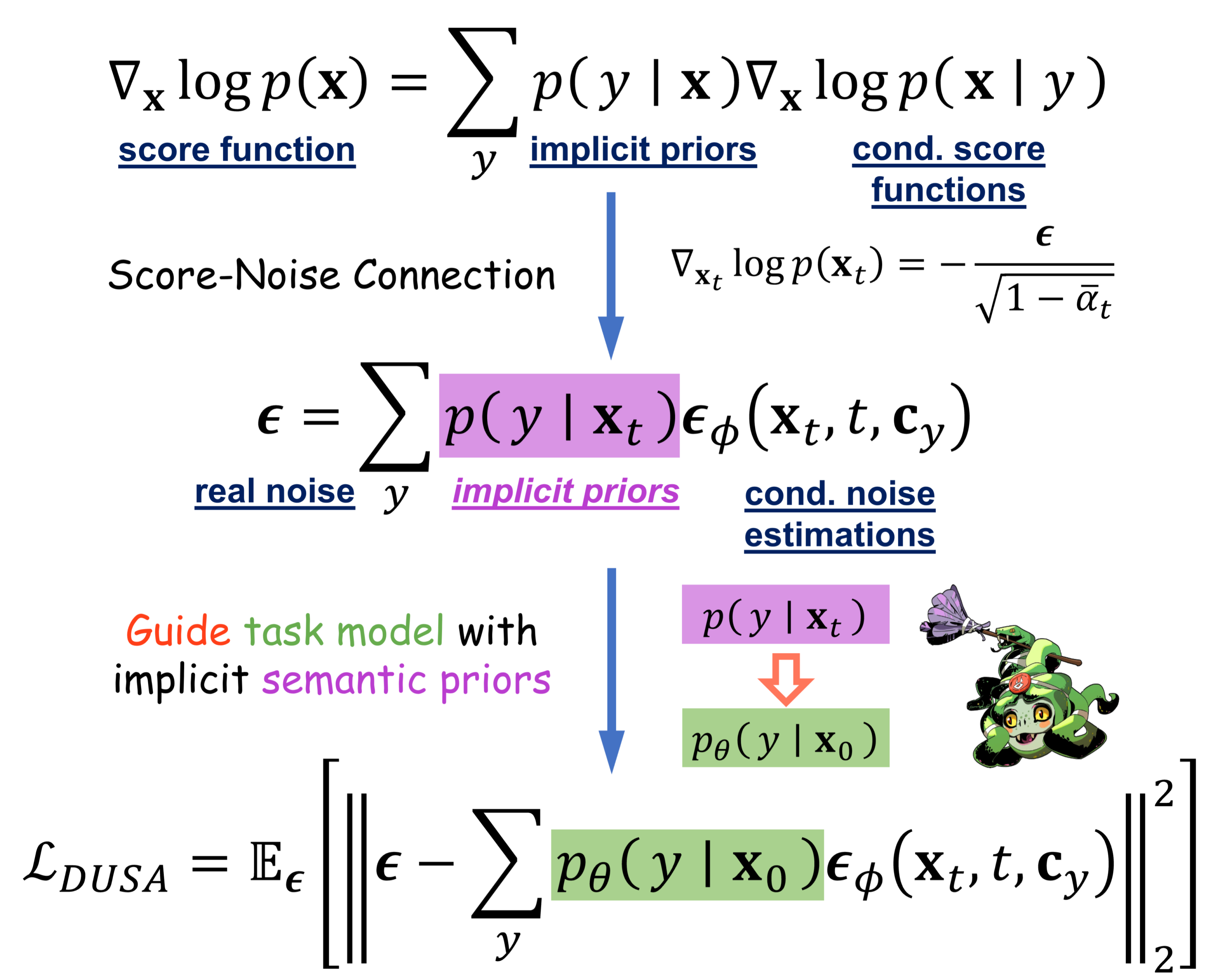
• The task model drains knowledge from the structured semantic priors underlying the diffusion model
• Both models are jointly updated with our DUSA objective
• A Candidate Selection Module (CSM) is proposed to improve adaptation efficiency

Theoretical Findings Semantic Structure of Score Functions We discover a semantic structure between score functions (i.e., \(\nabla_x\log p(x)\)) under mild assumptions about the densities: \[\nabla_\mathbf{x}\log p(\mathbf{x}) = \sum_y p(y\mid\mathbf{x}) \nabla_\mathbf{x}\log p(\mathbf{x}\mid y)\] This formula unveils that the unconditional score function \(\nabla_\mathbf{x}\log p(\mathbf{x})\) can be decomposed as a weighted sum of conditional score functions \(\nabla_\mathbf{x}\log p(\mathbf{x}\mid y)\), where the weights are given by the posterior probabilities \(p(y\mid\mathbf{x})\). Implicit Priors in Diffusion Models With Tweedie’s Formula we have \(\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t)=-\mathbf{\epsilon}/\sqrt{1-\bar{\alpha}_t}\), and a semantic structure emerges within diffusion models: \[\mathbf{\epsilon} = \sum_y p(y\mid\mathbf{x}_t)\mathbf{\epsilon}_\phi(\mathbf{x}_t,t,c_y)\] We highlight that \(p(y\mid\mathbf{x}_t)\) are not directly modeled, and can thus be seen as the implicit priors hidden in diffusion models. Test-time Adaptation with Structured Semantic Priors Given a task model \(f_\theta\) and a diffusion model \(\mathbf{\epsilon}_\phi\), we can embed task model prediction \(p_\theta(y\mid\mathbf{x}_0)\) to extract knowledge from the implicit priors \(p(y\mid\mathbf{x}_t)\): \[\mathcal{L}_{DUSA}(\theta,\phi)=\mathbb{E}_{\mathbf{\epsilon}}\Big[\big\Vert \mathbf{\epsilon} - \sum_yp_\theta(y\mid\mathbf{x}_0)\mathbf{\epsilon}_\phi(\mathbf{x}_t,t,c_y) \big\Vert_2^2\Big]\] Quantitative Results Fully Test-time Adaptation of ImageNet Classifiers Qualitative Results Fully Test-time Adaptation of ACDC Segmentors BibTeX